In my childhood me and my friends used to guess what would be the soccer Dream Team of the season. We hadn’t any metrics to compare our choices, so the results were doubtful.
Recently, I found this dataset about FIFA on Kaggle. The data contains the scores of 18.279 players in all of the 27 soccer positions (goalkeeper, centre forward, etc).
Motivated by my childhood I used this data and Linear Programming (LP) to find the set of players which sum maximizes the overall team score, in other words, the Dream Team.
4-4-2 or 4-3-3? What would be the formation of the Dream Team? To be more realistic, I assumed that this team has one of the formations from the post The Best FIFA 20 Formation for FIFA Ultimate Team by FIFA U Team.
Any additional information about teams, statistics, first choice players and formations was extracted in SoFIFA.
Linear Programming (LP)
The main idea of Linear Programming is to maximize (or minimize) an objetive function subject to constraints given by inequalities and/or equations which represents the rules of the problem.
In this problem, we have a particular case of LP called Integer Linear Programming (ILP), in which all variables of the problem are integers, the same case as in the classic Travelling Salesman Problem.
Beside solve logistic problems - find the route which minimal distance -, the LP are applied in others situations as:
- Cutting Stock Problem: The goal is to cut standard-sized pieces of stock material, such as paper rolls or sheet metal, into pieces of specified sizes while minimizing material wasted;
- Portfolio Optimization: The goal is to find the best portfolio, out of the set of all portfolios being considered, according to some objective, such as maximize the expected return or minimize the financial risk;
- The Diet Problem: The goal is to select a set of foods that will satisfy a set of daily nutritional requirement at minimum cost.
Proposed model
The problem is to find which players are in the Dream Team and their positions. Since each player has a score associated at each position, the idea is to create a dummy variable, 1 if the player is in that position and 0 otherwise. We have two matrices:
- $\mathbf{X}$: Matrix of variables;
- $\mathbf{W}$: Matrix which represents the scores of players in each position.
\begin{equation}
\mathbf{X} =
\begin{bmatrix}
x_{1,1} & x_{1,2} & \dots & x_{1,27} \\
x_{2,1} & x_{2,2} & \dots & x_{2,27} \\
\vdots & \vdots & \ddots & \vdots \\
x_{18279,1} & x_{18279,2} & \dots & x_{18279,27} \\
\end{bmatrix}
\quad
\mathbf{W} =
\begin{bmatrix}
89 & 89 & \dots & 0 \\
91 & 89 & \dots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \dots & 89
\end{bmatrix}
\end{equation}
The objetive function is:
\begin{equation} \max \sum_{i=1}^{18279} \sum_{j=1}^{27} w_{ij} \cdot x_{ij} \end{equation}
And we have the constraints:
\begin{align}
\sum_{i=1}^{18279}\sum_{j=1}^{27} x_{ij} & = 11 \label{eq: 11 players} \tag{1} \\
\sum_{j=1}^{27} x_{ij} & \le 1, \quad i = 1, \dots, 18279 \label{eq: unique position} \tag{2} \\
\sum_{k=1}^{23} b_{k} & = 1 \label{eq: unique formation} \tag{3} \\
\sum_{i=1}^{18279} x_{ij} - p_{kj} + (1 - b_k) \cdot M & \ge 0, \quad \begin{cases} j = 1, \dots, 27 \\ k = 1, \dots, 23 \\ M \ge \max p_{kj} \label{eq: players formation} \tag{4} \end{cases} \\
\end{align}
-
$\eqref{eq: 11 players}$, the Dream Team must have 11 players;
-
$\eqref{eq: unique position}$, each player must be in only one position;
-
$\eqref{eq: unique formation}$, the Dream Team has only one formation. $b_k$ is a dummy variable, which assumes 1 if the Dream Team are in the formation of index $k$, 0 otherwise;
-
$\eqref{eq: players formation}$, the formation is set given the distribution of players in each position. This constraint grants that players assume a formation. $p_{kj}$ is the number of players that need to be in the $j$-th position of formation $k$ and $M$ is a constant that validatidate the inequation.
Results
The players and the formation of Dream Team are in the bellow image. An interesting result is four players - L. Messi, E. Hazard, M. Salah and Neymar Jr - were in a different position than their favorite positions, this result suggests these players can perform better than players whose plays mainly in these positions. In short, L. Messi, E. Hazard, M. Salah and Neymar Jr are flexible players.
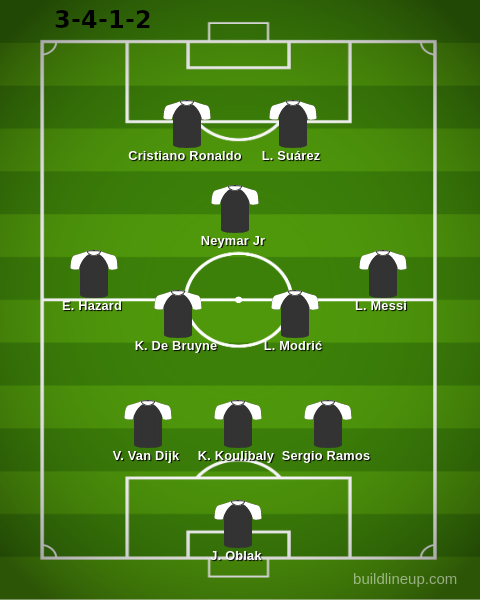
| Player | Score | Position | Current team |
|---|---|---|---|
| J. Oblak | 91 | GK | Atlético Madrid |
| V. Van Dijk | 90 | CB | Liverpool |
| K. Koulibaly | 89 | CB | Napoli |
| Sergio Ramos | 90 | CB | Real Madrid |
| E. Hazard | 92 | LM | Real Madrid |
| K. De Bruyne | 90 | CM | Manchester City |
| L. Modrić | 90 | CM | Real Madrid |
| L. Messi | 94 | RM | FC Barcelona |
| Neymar Jr | 93 | CAM | Paris Saint-Germain |
| Cristiano Ronaldo | 94 | ST | Juventus |
| L. Suárez | 91 | ST | FC Barcelona |
Comparing the Dream Team with the best team in FIFA (Real Madrid) we have the following results:
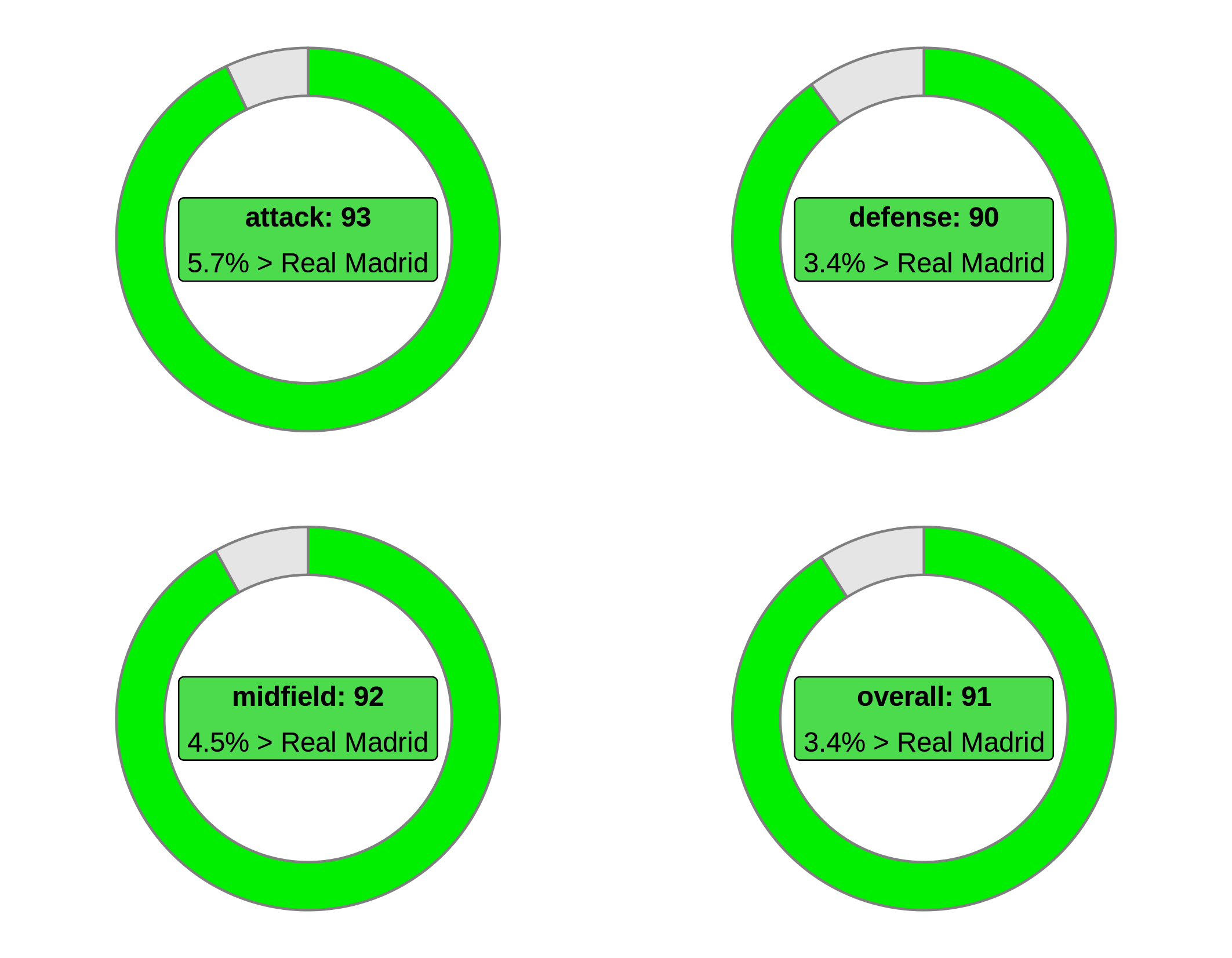
All the codes in this post and the solution was designed using R and are available in this repository on GitHub.
Feel free to comment or to send me an email.
